This is one of the optimization algorithm where we try lot of options and optimize (maximize or minimize based on the requirement) the output. For this algorithm, we will be given list of items, their size/weight and their values. We have a knapsack (bag pack) with a limited size/weight and we need to find the best choice of items to fit those in the knapsack so that we can maximize the value.
One of the examples where we can use this algorithm is while preparing for travelling (back packing for trekking or etc). We wish we can take everything but we will have limited backpack and need to choose the best items. One other classic example is a thief trying to rob a house or a shop. He can carry limited items and he needs to take the best choice so that he can maximize the value. (If he is a programmer, I am sure he will use this algorithm ;))
Here we will discuss only the classic flavor of knapsack problem, which is called 0-1 knapsack. It means, we can either take the full item or not. We can’t take the part of the item available.
Problem
Let us formalize the problem statement here. The input contains three parameters, price[], weights[] and sackCapacity.
- price[] – this array contains the prices/values of items
- weights[] – this array holds the weights/size of the items
- sackCapacity – this is the knapsack (backpack) capacity
So price[i] contains the price of ith item and weights[i] is the weight.
Solution
This knapsack problem can be solved with different approaches, but here we will explore the approach by an algorithm called Dynamic Programming (DP).
DP is all about breaking the original problem into sub problems, solving them and remember/store the solutions and then building the solution for original problem. In this case, we will find the best suitable or choice of items for weights from 1 to sackCapacity-1 and then we can easily build the solution for sackCapacity.
There are two different DP approaches,
- Top down DP (Recursive) – here we start calculating solution for original problem using solutions of sub problems and where the solutions for sub problems are achieved by performing recursive calls.
- Bottom up approach (Iterative) – here we find the solutions to smaller problems and then iteratively build the solution for original problem. For example, to calculate the Nth Fibonacci number, we start from finding 0, 1, 2 … N-1 Fibonacci numbers and then build Nth Fibonacci number. There are no recursive calls in this.
Even most of the modern computers perform poorly if Top down approach is used as it uses stack memory for recursive calls so here we will discuss the bottom up approach. As most of the DP approaches are better explained using examples rather than the algorithm itself, we will also follow the same approach to understand it better.
In simple words, we check each item and see whether we are getting the better value if we include this item in the knapsack, if yes, then take that item. If not, then skip this item.
Example
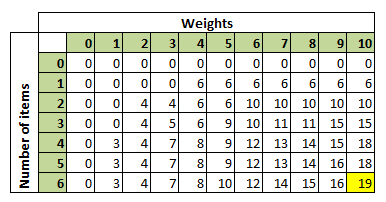
Total items – 6
Prices – {6, 4, 5, 3, 9, 7}
Weights – {4, 2, 3, 1, 6, 4}
Knapsack capacity – 10
So here all of our sub problems are – knapsack capacity with 0, 1 2, 3, 4, 5, 6, 7, 8, 9 and original problem is for knapsack capacity with 10.
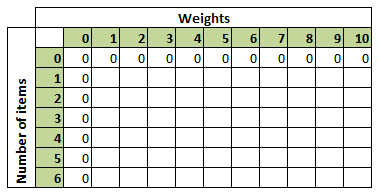
As per the DP, we need to find the solutions for these sub problems and store them in a table. For this, we can take a double dimension array – int[nItems +1][sackCapacity+1] (let us call it dpTable) where nItems is the number of items and sackCapacity is the knapsack capacity. In this, dpTable[i][w] – represents the optimal solution for i items for sack capacity weight w.
Then we need to initialize the array with 0 for first row and column as optimal solutions for 0 items with any sack capacity is zero and also for any number of items with 0 sack capacity. After the initialization, the dpTable looks like below.
Then, we perform the following steps iteratively for sack capacity from 1 to 10 (sackCapacity)
- Check the weight of the each item, if it can’t fit (weights[i] > w) into our sack, then we move to the next weight
- If we can fit it in (weights[i] <= w), then we calculate the optimal price by the following steps.
- Find the price if we include this item. We just wanted to know what the price gain is if we include this in the sack. So price = price of this item + price of (sackCapacity of this sub problem – weight of this item)
- Find the price if we don’t include this item – it will be optimal price of i-1 items.
- Then take the best option from above – the greater price.
So the final dpTable will look like below for the above example.
Algorithm in Java
Following method shows the implementation of how we perform the above mentioned steps to pick the optimal items.
/**
* price[] - value - $$$ Gain weights[] - weights sackCapacity - the maximum
* weight knapsack can carry.
*/
private static boolean[][] getItemsToPick(int[] price, int[] weights, int sackCapacity) {
int nItems = price.length;
//dp[i][w] - the maximum value of sub problem with i items and with w sack capacity.
//no need to initialize with zeros as in java, the defalt values are 0 for int premitive type.
int[][] dpTable = new int[nItems + 1][sackCapacity + 1];
boolean[][] keep = new boolean[nItems][sackCapacity + 1];
//iterate through all of the items
for (int i = 1; i <= nItems; i++) {
//calculate sub problem for all weights
for (int w = 1; w <= sackCapacity; w++) {
if (weights[i - 1] > w) {
// we cannt take this weight as it exceeds sub problem with weight w and i items
dpTable[i][w] = dpTable[i - 1][w];
} else {
//Price if we include item i
int pYes = price[i - 1] + dpTable[i - 1][w - weights[i - 1]];
//Price if we include item i
int pNo = dpTable[i - 1][w];
if (pYes > pNo) {
//this item MAY go into sack
keep[i - 1][w] = true;
dpTable[i][w] = pYes;
} else {
dpTable[i][w] = pNo;
}
}
}
}
//printing dpTable
System.out.println(Arrays.deepToString(dpTable));
return keep;
}
To print what items we picked, we need to keep track these choices in another boolean array. For this, we have used boolean[][] keep. Following java code backtracks the items we picked up and prints the details.
public static void printSelectedItems(boolean[][] keep, int sackCapacity, int[] price, int[] weights) {
//printing what items we picked
System.out.println("Selected items:");
int K = sackCapacity;
int n = price.length;
int wsel = 0;
int vsel = 0;
for (int i = n - 1; i >= 0; i--) { // need to go in the reverse order
if (keep[i][K] == true) {
System.out.println(i + "\tv=" + price[i] + "\tw=" + weights[i]);
wsel += weights[i];
vsel += price[i];
K = K - weights[i];
}
}
System.out.println("The overall value of selected items is " + vsel + " and weight " + wsel);
System.out.println("Maximum weight was " + sackCapacity);
}
Time Complexity
- The time complexity is O(NW). Here N – is the number of items and W is the weight of the knapsack. As it is depends on number of items and also on weights, we call this pseudo polynomial. It is linear in terms of number of items but remember, W – the sack capacity can be much much bigger than N. so this is called pseudo-polynomial.
- Space, we used O(N2) to store the DP table and same memory to keep track of what items we picked up. Actually we don’t need to have this extra keep table to backtrack items we picked up.
Following is the full java implementation of the above approach.
package com.sada.algorithms.dp;
import java.util.Arrays;
/**
* Knapsack algorithm
*
* @author Sada Kurapati <sadakurapati@gmail.com>
*/
public class Knapsack {
public static void main(String[] args) {
int[] price = {6, 4, 5, 3, 9, 7};
int[] weights = {4, 2, 3, 1, 6, 4};
int sackCapacity = 10;
boolean[][] keep = getItemsToPick(price, weights, sackCapacity);
printSelectedItems(keep, sackCapacity, price, weights);
}
/**
* price[] - value - $$$ Gain weights[] - weights sackCapacity - the maximum
* weight knapsack can carry.
*/
private static boolean[][] getItemsToPick(int[] price, int[] weights, int sackCapacity) {
int nItems = price.length;
//dp[i][w] - the maximum value of sub problem with i items and with w sack capacity.
//no need to initialize with zeros as in java, the defalt values are 0 for int premitive type.
int[][] dpTable = new int[nItems + 1][sackCapacity + 1];
boolean[][] keep = new boolean[nItems][sackCapacity + 1];
//iterate through all of the items
for (int i = 1; i <= nItems; i++) {
//calculate sub problem for all weights
for (int w = 1; w <= sackCapacity; w++) {
if (weights[i - 1] > w) {
// we cannt take this weight as it exceeds sub problem with weight w and i items
dpTable[i][w] = dpTable[i - 1][w];
} else {
//Price if we include item i
int pYes = price[i - 1] + dpTable[i - 1][w - weights[i - 1]];
//Price if we include item i
int pNo = dpTable[i - 1][w];
if (pYes > pNo) {
//this item MAY go into sack
keep[i - 1][w] = true;
dpTable[i][w] = pYes;
} else {
dpTable[i][w] = pNo;
}
}
}
}
//printing dpTable
System.out.println(Arrays.deepToString(dpTable));
return keep;
}
public static void printSelectedItems(boolean[][] keep, int sackCapacity, int[] price, int[] weights) {
//printing what items we picked
System.out.println("Selected items:");
int K = sackCapacity;
int n = price.length;
int wsel = 0;
int vsel = 0;
for (int i = n - 1; i >= 0; i--) { // need to go in the reverse order
if (keep[i][K] == true) {
System.out.println(i + "\tv=" + price[i] + "\tw=" + weights[i]);
wsel += weights[i];
vsel += price[i];
K = K - weights[i];
}
}
System.out.println("The overall value of selected items is " + vsel + " and weight " + wsel);
System.out.println("Maximum weight was " + sackCapacity);
}
}